GradNorm

论文地址

GradNorm: Gradient Normalization for Adaptive Loss Balancing in Deep Multitask Networks

论文总结

GradNorm 是一种用于多任务学习中自动调整任务权重的算法。

《GradNorm: Gradient Normalization for Adaptive Loss Balancing in Deep Multitask Networks》论文总结

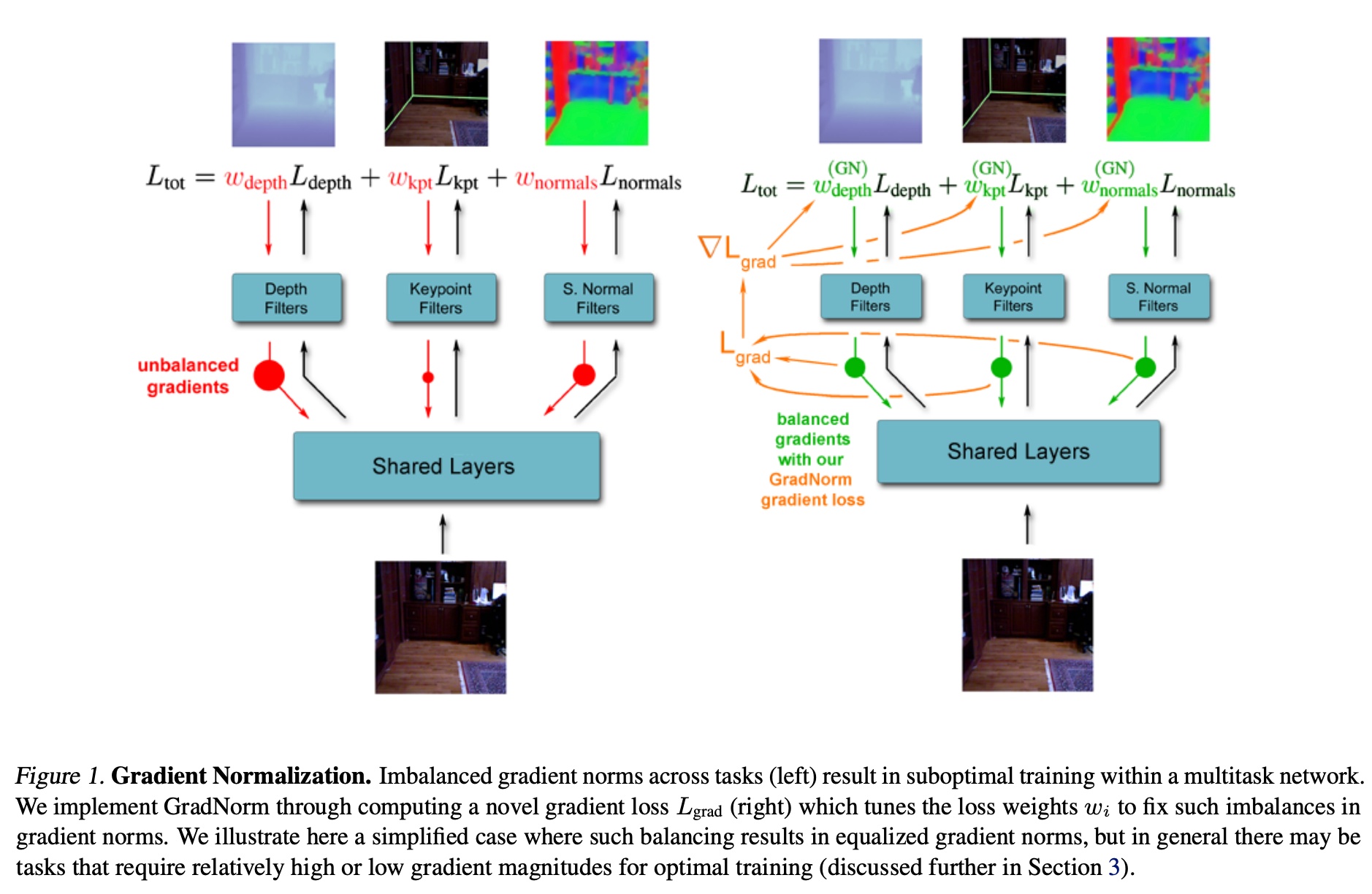
• 摘要：提出了一种用于深度多任务网络的梯度归一化（GradNorm）算法，通过动态调整梯度幅度自动平衡深度多任务模型的训练，提高了准确性并减少了过拟合，展示了梯度操纵对多任务网络训练动态的强大控制能力。

• 引言：

  • 多任务学习能使一个模型同时执行多个感知任务，提高效率和性能，但训练困难，需要平衡不同任务。
  • 以往的方法通过操纵网络的前向传播来寻找平衡，但忽略了任务不平衡会导致反向传播梯度不平衡的关键问题。
  • 本文通过调整多任务损失函数的梯度幅度来解决此问题，提出的自适应方法中损失函数的权重$w_i$在每个训练步骤$t$可变。
  • GradNorm算法通过惩罚梯度过大或过小的网络来优化权重$w_i(t)$以平衡梯度，类似于批归一化，但在任务间而非数据批间进行归一化，并以速率平衡为目标。

• 相关工作：

  • 多任务学习在深度学习之前就已存在，近期深度学习的发展使其重新受到关注，在计算机视觉、自然语言处理、语音合成等多个领域有应用。
  • 相关工作包括寻找利用多任务模型中任务关系的明确方法，如聚类方法、深度关系网络和交叉缝合网络等，以及根据任务内在不确定性推导任务权重的联合似然公式。

• GradNorm算法：

  • 定义和预备知识：

    • 定义了与梯度相关的量，包括子集$W$、梯度范数$G_W^{(i)}(t)$、平均梯度范数$\bar{G}_W(t)$，以及各种训练速率，如损失比$\tilde{L}_i(t)$、相对逆训练速率$r_i(t)$。

      • 用GradNorm平衡梯度：

    • 通过平均梯度范数$\bar{G}_W(t)$为梯度建立共同尺度，利用相对逆训练速率$r_i(t)$平衡不同任务的训练速率。

    • 目标梯度范数为$G_W^{(i)}(t) \mapsto \overline{G}_W(t) \times\left[r_i(t)\right]^{\alpha}$，其中$\alpha$是额外的超参数，用于调整恢复力的强度。
    • GradNorm通过$L_1$损失函数$L_{grad}$实现，计算实际和目标梯度范数之间的差异，对损失$L_{grad}$求导并更新权重$w_i(t)$，同时对权重进行重归一化以解耦梯度归一化与全局学习率的关系。

GradNorm示意图

• 玩具示例：

  • 构建了多任务网络的常见场景，即训练具有相似损失函数但不同损失尺度的任务。
  • 当$w_i(t) = 1$时，网络训练会被具有较大损失尺度的任务主导，GradNorm通过增加较小$\sigma_i$任务的$w_0(t)$来克服此问题，提高了测试性能，且比不确定性加权更稳定。
  • GradNorm运行中每个$w_i(t)$的轨迹稳定且收敛，时间平均权重$E_t[w_i(t)]$接近最优静态权重，可简化繁琐的网格搜索过程。

• 在大型真实世界数据集上的应用：

  • 数据集和模型：

    • 使用两个变体的NYUv2数据集，包括NYUv2 + seg和NYUv2 + kpts。

    • 尝试两种不同的模型：SegNet网络和FCN网络，使用标准的像素级损失函数，所有模型参数在最后一层之前共享。

      • 主要结果：

    • GradNorm在NYUv2 + seg数据集上提高了所有三个任务的性能，超过了等权重基线，并接近或超过了单网络的最佳性能。

    • 在NYUv2 + kpts数据集上，GradNorm网络也优于其他多任务方法，匹配或超过了单任务网络的性能。

    • GradNorm通过积极的速率平衡实现了更好的测试性能，同时抑制了某些任务的权重，如深度任务的$w_{depth}(t)$。

      • 找到最优网格搜索权重：

    • 通过训练100个随机任务权重的网络并与GradNorm网络比较，发现GradNorm在一次训练中找到了最优网格搜索权重，网络性能与到时间平均GradNorm权重的距离有很强的负相关。

  • 调整不对称性$\alpha$的影响：

    • $\alpha$是算法的唯一超参数，NYUv2的最优值约为$\alpha = 1.5$，在高度对称的玩具示例中使用$\alpha = 0.12$。
    • 调整$\alpha$可带来性能提升，几乎任何$0 < \alpha < 3$的值都能提高网络性能，较高的$\alpha$值会使权重$w_i(t)$分得更开，减少过拟合或学习过快任务的影响。

  • 定性结果：

    • GradNorm在定量改进显著的任务中产生了优越的视觉结果。

• 结论：

  • GradNorm基于平衡不同任务的训练速率来调整多任务学习中的损失权重，在合成和真实数据集上均提高了多任务测试性能。
  • GradNorm通过超参数$\alpha$适应不同任务的不对称性，性能优于其他多任务自适应加权方法，可匹配或超越详尽网格搜索的性能，且耗时更少。
  • 希望将GradNorm扩展到其他应用场景，认为梯度调整对于训练复杂任务的大型有效模型至关重要。

GradNorm算法说明

一、背景和动机

在多任务学习中，不同任务的损失函数通常具有不同的尺度和重要性。如果不对这些任务进行平衡，可能会导致某些任务主导学习过程，而其他任务得不到充分学习。GradNorm 算法旨在自动平衡多任务学习中的不同任务，通过调整任务权重来实现各个任务的均衡学习。

二、算法原理

1. 计算梯度范数

   • 对于每个任务，计算其损失函数相对于模型参数的梯度。然后计算该梯度的范数，表示该任务在当前参数下的学习进度。

2. 定义参考梯度范数

   • 定义一个参考梯度范数，通常是所有任务梯度范数的平均值。这个参考范数代表了整体任务的平均学习进度。

3. 计算梯度范数偏差

   • 对于每个任务，计算其梯度范数与参考梯度范数的偏差。这个偏差反映了该任务相对于整体平均进度的快慢程度。

4. 更新任务权重

   • 根据任务的梯度范数偏差来更新任务权重。如果一个任务的梯度范数偏差较大，说明它的学习进度与平均进度相差较大，需要调整其权重以使其学习速度与其他任务更加平衡。

   • 具体的更新公式通常涉及到一些超参数，如学习率等。更新后的任务权重用于计算多任务学习的总损失函数，从而影响模型的参数更新。

三、算法流程

1. 初始化模型参数和任务权重。

2. 在每个训练迭代中：

   • 计算每个任务的损失函数。
   • 计算损失函数相对于模型参数的梯度。
   • 计算每个任务的梯度范数。
   • 计算参考梯度范数。
   • 计算每个任务的梯度范数偏差。
   • 根据偏差更新任务权重。
   • 使用更新后的任务权重计算总损失函数，并更新模型参数。

3. 重复步骤 2 直到模型收敛。

四、应用场景

1. 多任务深度学习

   • 在深度学习中，同时学习多个相关任务时，可以使用 GradNorm 算法自动平衡不同任务的学习进度，提高模型的整体性能。例如，在图像识别中同时学习图像分类、目标检测和语义分割等多个任务。

2. 强化学习多任务场景

   • 在强化学习中，如果智能体需要同时完成多个任务，可以使用 GradNorm 来平衡不同任务的奖励信号，使智能体能够更好地学习多个任务的策略。

五、优势和不足

1. 优势

   • 自动调整任务权重，减少了人工调参的工作量。
   • 能够有效地平衡多任务学习中的不同任务，提高模型的泛化能力和性能。
   • 适用于各种多任务学习场景，具有较强的通用性。

2. 不足

   • 需要计算每个任务的梯度范数，增加了一定的计算复杂度。
   • 超参数的选择对算法性能有一定影响，需要进行适当的调参。