截断正态分布

目录

截断正态分布（Truncated normal distribution）

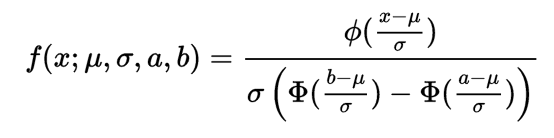
python生成正态分布

import numpy as np
np.random.normal(0, 0.1, 10)

截断正态分布（Truncated Normal Distribution）是一种在统计学中具有重要应用的概率分布，以下是关于它的详细介绍：

定义

设$X$是一个服从正态分布$N(\mu,\sigma^{2})$的随机变量，如果将$X$的取值范围限制在$[a,b]$内，那么$X$在$[a,b]$上的分布就称为截断正态分布。也就是说，只考虑正态分布在某一区间内的部分，而将该区间之外的概率质量“截断”掉。

概率密度函数

截断正态分布的概率密度函数为：

$$f(x;\mu,\sigma,a,b)=\frac{\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x - \mu)^{2}}{2\sigma^{2}}}}{\Phi(\frac{b-\mu}{\sigma})-\Phi(\frac{a-\mu}{\sigma})}, \quad a\leq x\leq b$$ 其中$\Phi(z)$是标准正态分布$N(0,1)$的累积分布函数，$\mu$是均值，$\sigma$是标准差，$a$和$b$分别是截断区间的下限和上限。

性质

• 均值和方差：截断正态分布的均值和方差与普通正态分布有所不同，它们取决于截断区间$[a,b]$以及原正态分布的参数$\mu$和$\sigma$。一般来说，计算截断正态分布的均值和方差需要用到积分等数学方法，其表达式较为复杂。

• 形状：与普通正态分布类似，截断正态分布的概率密度函数也是单峰的，但由于截断的影响，其形状可能会在截断点附近发生变化，不再像普通正态分布那样具有完全对称的钟形曲线。在截断区间内，它仍然保持着正态分布的一些特征，但在截断点处会出现“截断”效应，导致概率密度函数在这些点处不连续。

应用

• 经济学：在对一些经济变量进行建模时，由于实际情况中变量的取值往往存在一定限制，截断正态分布可以更准确地描述这些变量的分布情况。例如，研究家庭收入分布时，可能会发现收入存在下限（如贫困线）和上限（如极高收入群体的边界），使用截断正态分布可以更好地拟合这种受限的收入分布数据。

• 生物学：在研究生物特征的分布时，也可能会遇到需要使用截断正态分布的情况。比如，某种生物的体长可能由于生存环境等因素，在一定范围内呈现出类似正态分布的特征，但超出某个范围的体长则很少出现，此时可以用截断正态分布来描述该生物体长的分布。

• 工程学：在质量控制和可靠性分析中，截断正态分布也有应用。例如，在生产过程中，产品的某些质量指标可能服从正态分布，但由于生产工艺或设计要求，只有在一定范围内的质量指标才是合格的，对这些合格产品的质量指标分布进行建模时，就可以使用截断正态分布。