目录
简介
隐马可尔可夫模型是一个生成模型,给定一个观察序列,HMMs 模型隐含一个与观察序列对应的状态序列。 HMMs的示意图如下:
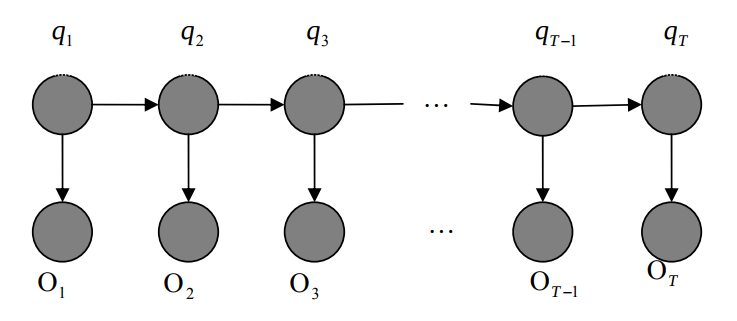
独立性假设
- t 时刻的状态只依赖于 t −1 时刻的状态
- t 时刻所生成的值只依赖于t 时刻的状态
- 状态与具体时间无关
2 => 两个假设
- 齐次马尔科夫性假设:状态只依赖与前一个时刻的状态,与当前时刻t无关,与其他时刻的状态和观测无关。
- 观测独立性假设:任意时刻的观测只依赖于当前时刻的状态,与其他时刻的状态和观测无关。
离散马尔科夫过程
- N个不同状态Si
- 状态转移概率矩阵A(n * n)
当随机过程满足:当前所处的状态仅与它之前的一个状态有关,该随机过程为马尔可夫随机过程。
5 => 五个要素
有时又称为三要素,去掉
- N,模型中的状态数
- M,每个状态不同的观察符号,即输出字符的个数,用V表示各个字符的集合
- A,状态转移概率分布
- B,观察字符在状态j时的概率分布
- π,初始状态分布
从以上的讨论可知,一个完整的隐马尔可夫模型要求两个具体的模型参数 N 和 M ,和三个概率矩阵 A, B,π ,也即隐马尔可夫模型可形式化定义为一个五元组( N, M , A, B,π )。
观测序列的生成过程
输入: λ=(A,B, π)
输出: 观测序列 O=(o1, ... , oT)
流程:
- 根据π生成初始状态
- 根据初始状态和观测概率矩阵,生成观测符号o
- 根据状态转义概率生成下一时刻的状态
- 如果产生了T个观测符号,则终止,没有则转2
3 => 三个基本问题
- 概率计算问题:根据模型λ=(A,B, π),判断某一观测序列出现的概率
- 学习问题:已知观测序列,求模型的参数,使得观测序列概率最大
- 预测问题:又称解码问题,给定模型和观测序列,求最大概率的状态序列
viterbi算法
viterbi算法只是解决隐马第三个问题(求观察序列的最可能的标注序列)的一种实现方式。